Probability,
Significance, Ranges
Until now I've been using probability
without really defining it. Why talk about probability, when events either
happen or they don't? A probability is an expression of how likely we think an event
is. Not a great definition, using 'likely' (you might say it's a circular
argument). Another definition is the fraction of times that an event would
occur if you repeated the experiment forever. So if you flipped a coin a
million times, you'd expect about half a million to be heads. The probability
of heads is half a million divided by a million, or 0.5, or 50%.
- What is the probability of getting a six on a six sided die?
(Answer: All of the
sides are equally likely, and there are six sides, so the answer is 1/6)
Now if we flip a
coin a million times, we'd expect about a half a million heads. But what if we
only flipped three or four times? Try it if you've got a coin. You probably
won't get two heads and two tails. You certainly won't get a head and a half.
That's the thing about probability and one of the pitfalls of statistics.
Let's say a tobacco
company, call them Fill Morse, wanted to prove to the public that their
cigarettes didn't cause cancer. Morse could get 5 smokers, find that one had
cancer, and then say: "80% of smokers of Fill Morse cigarettes don't get
cancer, new study says." This doesn't give a measure of the true
probability of cancer incidence in smokers.
- What kind of study would be needed to come to a conclusion about
cancer? What evidence would be needed, what comparisons would need to be
made?
Statisticians talk
about probability distributions. Especially, they talk about the normal
distribution, or the (ready for it now) bell curve. One of the ideas in
statistics is that if you have a huge group of samples and the variation
between them is small (like if you measured the heights of north american men,
say), it has a normal distribution. This means that the mean, median, and mode
are the same value, and have the highest probability of occurring, with lower
and lower probabilities as you go farther away from the mean (in other words,
most men are 'average' height, and really really tall or really really short
men are rare).
- Is the distribution of wealth normal? Is the distribution of
income? (Hint: do most people have an 'average' income or wealth, if
average is mean?)
The normal distribution looks like this—this
one has a mean of zero, a standard deviation of ten.
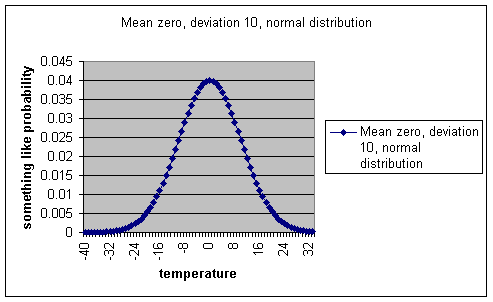
But there are different kinds of normal
distributions. The temperature in two cities might both have normal
distributions, with similar mean temperatures, but the weather in one city,
call it Varia, could be much more variable than in another city, call it
Steadia. The two distributions might
look like this:
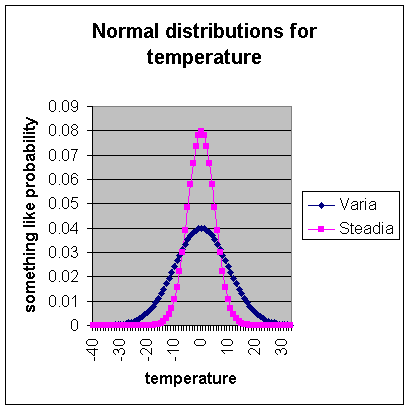
The point is that an average, by itself,
doesn't say very much at all (as you knew from the discussion on averages
above). That's why statisticians talk about the standard deviation and
the significance.
Let's look at another example. Opinion polls
are conducted all the time, which ask "do you support the bombing of
helpless country x" or some such thing. Results are something like 60% no,
40% yes. And the fine print was something like "results are valid to
within 1% 19 times out of 20".
The 1% is the deviation. The 19 times out of
20 is the significance.
What this means is that if you took another
test, there would be 95% chance (19 out of 20) that the answer would come out
between 59-61% no and 39-41% yes. In other words, the pollers are pretty
confident that their sample is not biased and that it represents the
population.
The standard deviation on the Stanford Binet
IQ test is 3. The test assumes a normal distribution. The normal distribution
means that the test told you you were worth 100 IQ points (idiotic to begin
with, of course), there is only a 68% chance that your 'real' IQ falls between
97 and 103. There's a 95% chance that your IQ falls between 94 and 106, and as
you increase the range, the chances go up that your value falls within the
range.
These are not the greatest explanations of
the phenomena but the point is that these figures, of standard deviation and
significance, are what tell you how much an average can be trusted. They are
hardly ever included with any statistics (except when the people giving them to
you are confident, like in opinion polls). Which means you can hardly trust an
average at all.